Sekhar Chandra Ray*
Department of Physics, College of Science, Engineering and Technology, University of South Africa, Private Bag X6, Florida, 1710, Science Campus, Christiaan de Wet and Pioneer Avenue, Florida Park, Johannesburg, South Africa
Frontier Research Today, 2018, 1:1002
Published Online: 20 September 2018 (Article)
DOI: 10.31716/frt.201801002
*Corresponding Author. Email: This email address is being protected from spambots. You need JavaScript enabled to view it. and This email address is being protected from spambots. You need JavaScript enabled to view it.
Abstract
We report an investigation into the magnetic and electronic properties of partially hydrogen functionalized vertically aligned few layers graphene (FLG) synthesized by microwave plasma enhanced chemical vapor deposition process. The FLG samples are hydrogenated at different substrate temperatures (50oC - 200oC) to alter the degree of hydrogenation and their depth profile. The unique morphology of the structure gives rise to a unique geometry in which graphane (full hydrogenation) / graphone (partial hydrogenation) is supported by graphene layers in the bulk, which is very different from other widely studied structures such as one-dimensional nanoribbons. Synchrotron based x-ray absorption fine structure spectroscopy measurements have been used to investigate the electronic structure and the underlying hydrogenation mechanism responsible for the magnetic properties. While ferromagnetic interactions seem to be predominant, the presence of antiferromagnetic interaction was also observed. Free spins available via the conversion of sp2 to sp3-hybridized structures and the possibility of unpaired electrons from defects induced upon hydrogenation are thought to be likely mechanisms for the observed ferromagnetic orders. Theoretical point of view different possible reason for the formation of magnetism in Graphene materials also discussed elaborately.
Keywords
Graphene; Graphone; Graphane; XANES; Magnetization; Magnetic hysteresis loop
1 Introduction
Graphene composed of a single-atomic layer of carbon atoms has emerged as fascinating example of designer materials, where dimensionality plays an important role and it has become a novel platform for the engineering of novel electronic and magnetic-storage devices.1-6 For spintronic applications, graphene is considered as a promising material due to its long spin relaxation time and length because of the small spin-orbit coupling of carbon atoms.5,6 Similar to the modulation of physical and chemical properties of carbon nanotubes, various strategies for modulating the electronic and magnetic properties of graphene have been proposed for versatile applications.7-9 Sofo et al predicted that fully hydrogenated graphene (graphane) could be a non-magnetic semiconductor with a band gap of 4.5 eV, which was later confirmed experimentally.7,8 Zhou et al predicted that semi-hydrogenated graphene sheet (graphone) can become ferromagnetic at room temperature with a band gap of 0.46 eV, which is much smaller than that of graphane (4.5 eV)9. This change in the band gap occurs via the formation of tetrahedral carbon (ta-C), which reduces the connectivity of the p-sheets of graphene and the π − π energy gap of the localized double bonds (i.e. the formation of an alternating sp2–sp3–sp2–sp3 hybridization pattern). Furthermore, calculations have also shown that hydrogen pairs arranged in lines can create semiconducting or metallic waveguides through confinement effects. A large band gap opening in hydrogen-covered regions would lead to an effective potential barrier for the electrons. Experimentally, disordered hydrogen adsorption has been shown to influence the transport properties in graphene through localization effects10, which may occur due to adsorption of hydrogen on free-standing graphene11, as well as on supported graphene layer.12,13 Zhou et al predicted that in semi-hydrogenated bi-layer graphene (referred as BL-graphone), the most stable configuration undergoes a (1x2) surface reconstruction14. The graphone (partial hydrogenation) sheet can be synthesized by supporting graphene first on a substrate followed by a hydrogenation process; otherwise removing of half of the hydrogen atoms from one surface of graphane.9,15 In this (graphone) process, the graphene leads to the formation of unpaired electrons and the remanent delocalized bonding network which is responsible for the formation of ferromagnetic materials with Curie temperatures between 278 K to 417 K and could be most promising materials for future spintronics applications.9,16 Since graphene, graphane and graphone individually show remarkable properties and are expected to have versatile electronic and magnetic device applications, it is a compelling study to investigate the electronic structure and magnetic properties when two of them bind each other like graphene-graphane and graphene-graphone bilayer structures. Remarkable properties extend to bilayer and few-layers graphene and even combination of graphene and graphone layers.14 When graphene and graphone both in single layer sheet bind together, metallic but nonmagnetic characteristics are formed as predicted theoretically by Zhou et al.14 They show that two pristine graphene sheets cannot be bonded together due to the prevailing weak van der Waals interaction. But, in presence of H the unsaturated C sites in the graphone sheet are reactive because of unpaired electrons. A graphene sheet can bind to graphone and the system can be viewed as semi-hydrogenated bi-layer graphene (BL-graphone) or simply graphene supported graphone.14 Furthermore at the interface between graphene and graphane, magnetism arising from the edges can be tuned.17
In this study, we have studied the graphene supported graphone/graphane bilayer structure to elucidate their electronic structure and magnetic behaviors with a view on spintonics applications. The magnetism in carbon-based materials is quite unique in itself as it arises from only s and p orbital electrons unlike the magnetism, which arises more intuitively from the 3d or 4f electrons in traditional magnetic materials. Using microwave plasma enhanced chemical vapor deposition, thin vertically aligned few layers graphene (FLG) nanoflakes were synthesized on bare Si(100) substrates, which were further subjected to hydrogen plasma treatment. The FLG samples are hydrogenated at different substrate temperatures to alter the hydrogenation depth and process. The particular morphology of the structures gives rise to a unique geometry in which graphane/graphone layers are supported by graphene layers in the bulk which is very different from other more widely studied structures such as one dimensional nanoribbons. The change in the electronic and magnetic properties was measured as a function of hydrogen content introduced in the structures and its temperature dependence using X-ray absorption, Raman spectroscopy and magnetic force microscopy. Field-dependent magnetization of representative samples was studied using a SQUID-type magnetometer. The work provides further knowledge and contributions to the emerging body of experimental and theoretical data related to magnetism in graphene and graphene based nanostructures.
2 Experimental details
2.1 Preparation of few layer graphene and hydrogen functionalized graphene
The synthesis of FLGs was carried out in a SEKI microwave plasma enhanced chemical vapor deposition system, equipped with a 1.5 kW, 2.45 GHz microwave source. The substrates used were bare n-type heavily doped Si wafers (resistivity < 0.005 Ω cm) (10 mm x 10 mm). Prior to growth, the substrates were pretreated with N2 plasma at 650 W at 40 Torr while the substrate temperature was maintained at 900°C. Synthesis was then carried out using CH4/N2 (gas flow ratio = 1:4) plasma at 800 W for a duration of 60 s. The samples were allowed to cool under a constant N2 flow. The conditions used were similar to the ones used in our previous publications.18-21 The hydrogen microwave plasma treatment of the FLGs was carried out at three different substrate temperatures of 50, 100 and 200°C at a chamber pressure of ~2 Torr with a treatment time of 90 s at a microwave power of 150 W.
2.2 Characterizations
Raman spectroscopy was performed using an ISA LabRam system equipped with a 632.8 nm He-Ne laser with a spot size of approximately 2-3 μm, yielding a spectral resolution of better than 2 cm-1. Due care was given to minimize sample heating by using a low laser power below 2 mW. The core-level XPS spectra were recorded on a KRATOS–SUPRA spectrometer at UNISA (Florida Science Campus), South Africa using monochromatic Al Kα radiation with excitation energy hν = 1486.6 eV having base pressure 1.2 x 10-8 Torr. The X-ray absorption near edge structure (XANES) spectra was obtained using the high-energy spherical grating monochromator 20A-beamline at the National Synchrotron Radiation Research Center (NSRRC), Hsinchu, Taiwan. XES and corresponding C K-edge XANES measurements were carried out at beamline-7.0.1 at the Advanced Light Source, Lawrence Berkeley National Laboratory. The energy resolutions of XES and XANES measurements were ∼0.35 and 0.1 eV, respectively. The magnetic properties of these samples were characterized by SQUID with sensitivity better than 5 x 10-8 emu. The topographical and magnetic force microscopy (MFM) measurements were carried out using a Veeco Dimension 3100 AFM connected to a Nanoscope IIIa controller in a tapping mode configuration. To detect magnetic domains in the prepared samples, low moment magnetic probes with Co/Cr coatings were used. To assess the correlation of surface features and assess the effects of magnetization, the topographic (height), amplitude and phase signals were imaged simultaneously for both conventional topographical imaging and magnetic measurements. MFM data was acquired while maintaining a constant lift scan height of ~10 nm above the topography (height) data to reduce coupling between Van der Waals and magnetic forces and also demonstrate the field strength generated by the magnetic domains. In addition, the electron field emissions (EFEs) were measured using a Keithley power supply.
3 Results and discussion
3.1 Surface Morphology and Electron Field Emission (EFE)
The scanning electron microscopy (SEM) images of pristine and hydrogenated FLGs (FLGs:H) are shown in Figure 1(a, b) and it is evident from them that the FLGs synthesized are vertically aligned to the underlying substrate and are randomly intercalated to each other forming a porous mesh like network. The H2 plasma treatment process does not disturb the vertically aligned nature of the graphene platelets; however, it leads to an increase in the sharp graphene edges throughout the graphene surfaces. It is found that the apparent thickness of the edges of graphene platelets is reduced due to plasma etching effects. Figure 1(c) plots the electron field emission (EFE) current density (J) as a function of the applied electric field (EA). The figure shows that there exists a threshold of electric field, beyond which J increases roughly exponentially. Fowler-Nordheim (F-N) plots as shown in Figure 1(d), is better illustrate the threshold electric field or turn-on electric field (ETOE). The ETOE were obtained with linear curve fitting in the high electric field region as shown in Figure 1(d), and were found to increase from 26.5 V/mm (pure FLGs) to 36.3 V/mm for FLGs:H@50oC (whereas 64.4 V/mm for FLGs:H@200oC) indicates that H-doping enhances three-dimensional sp3 bonding configuration.22 These observation clearly indicated that hydrogen is functionalized on the surface of FLG.
Figure 1. SEM images of (a) pristine and (b) hydrogenated FLGs (FLGs:H@500C) showing the increase in the disorder. (c) Electron Field Emission of FLGs and FLGs:H and (d) F-N plot
3.2 Raman Spectroscopy
The Raman spectrum of pristine FLGs and hydrogen plasma treated FLGs treated at different temperatures is shown in Figure 2(a). The Raman spectrum of the pristine FLGs displays three characteristic peaks: D band at ~1335 cm-1, G band at ~1583 cm- 1 and 2D band at ~2664 cm-1. Post hydrogen-plasma treatment, the Raman spectra of the FLG changes significantly with the increase in the intensities of peaks at 1617 cm-1, 2462 cm- 1 and 2920 cm- 1. The peaks at ~2460 and 2920 cm-1 arise via a combination of (D+D′) bands and are defect activated.23-26 The D peak too is defect activated via an inter-valley double resonance process and its intensity provides a convenient measure for the amount of disorder.23-27 The D peak is enhanced after hydrogenation and is due to hydrogen attachment, which breaks the translational symmetry of C=C sp2 bonding.28 Upon hydrogenation, the 2D band of FLG:H also becomes intense and shows a red-shift accompanied by a change in the I2D/IG ratio [Figure 2(b)]. Now, the position and peak intensities of G and 2D band can be used as a fingerprint for mono, bi-, tri- or multilayered graphene.23 When compared to pristine FLGs, the hydrogenated samples show a shift from 2664 to 2660 cm-1, signifying the formation of bi- or tri- layer graphene23,27 This reduction in the number of graphene-layers is further confirmed from the intensity ratio of the 2D and G peaks. It is observed that the (I2D/IG) ratio changes from 0.75 (FLG)→1.1 (FLG:H@50oC)→0.80 (FLG:H@100oC→0.85 (FLG:H@200oC). A I2D/IG ratio of >1 is indicative of formation of bi-layer graphene, whereas an I2D/IG ratio of <1 represents tri- or multilayered graphene.28 The increase in the intensity of D band (at 50oC) along with the presence of a new band at ~1617 cm-1 (denoted as D′) can be attributed to the attachment of hydrogen species on the top layer or the inter-layer of FLGs. As compared to pristine FLGs, the FLG:H show an increase in the intensity of D, 2D and (D+D′) bands owing to the break in the translational symmetry of C-C sp2 bonds and the formation of C-H sp3 bonds.26 The features and peak position of D and 2D of our non-hydrogenated graphene identifies as FLG; whereas hydrogen functionalized graphene (FLG:H) identifies as bi- or tri-layer graphene. Also, with an increase in the hydrogenation temperature, the G-band shifts by ~3 cm-1, caused due to a change in charge density.29,30 A similar reduction in the number of graphene layers upon hydrogen plasma treatment has been observed in the past as well.31
Figure 2. (a) Raman spectra of pristine and FLGs hydrogenated at different temperatures, (b) the red-shift of G and G` (2D) peaks upon hydrogenation at different temperatures.
Since, the FLGs are vertically aligned on a Si-substrate, it is expected only the top-most surfaces of the FLGs would be predominantly accessible to atomic hydrogen. At low temperature (50oC in the present case), the hydrogen-plasma exposure is not expected to result in graphane where the hydrogen atoms are attached on both sides of the graphene sheet. The microwave plasma system used in the work is operated at a moderate pressure (2 Torr) and a relative high power density (14 Wcm-3) as compared to capacitively coupled radio frequency systems (1 Torr/0.03 Wcm-3) used in other studies.16 At higher temperatures (100oC - 200oC) powers, it can be expected that the various species generated (H+, H3+ and hydrogen radicals) are able to passivate/percolate through the top layer and form C-H bonds with the subsequent underlying graphene layers. Also, at higher temperatures (100oC - 200oC), the graphene flakes are functionalized and annealed simultaneously. Luo et al. observed that the annealing process for graphene starts above 75oC and is completed at 350oC with a long annealing duration.32 If the hydrogenation and annealing is occurring simultaneously at 100oC / 200oC temperatures, then it is expected that C-H bonds will be formed in the inner layers of the FLGs, once the top surface of the FLGs has been hydrogen passivated. The 2D band of hydrogen functionalized FLG is very sharp, strong and red-shifted compared to pure FLG indicative of the reduction in the number of graphene layers.23,27
3.3 Electronic Structure and Bonding Properties
For graphitic materials, in general, the XANES spectra can be subdivided into three regions characterized by specific resonance energy.33 The first region of π* resonance appears around 285±1 eV, the C-H* resonance around 288±1 eV, and a broad region between 290 eV – 315 eV corresponding to σ* resonance. The presence of the π* and C-H* resonances serve as a fingerprint for the existence of sp2 hybridized C-C bonds and C-H bonds, respectively. The C K-edge XANES spectra of the samples (Figure 3) shows the features at ~285.1 (±1) eV, ~292.6 (±1) eV and ~291.6 (±1) eV which can be attributed to the unoccupied 1s→π*, 1s→σ* and excitonic states transitions, respectively.33 While, the peak positions for FLG:H@50oC are similar to that of pristine FLGs, the absorption edges are shifted towards lower energy level for FLG:H@100oC (200oC) [285.3 eV (FLG & FLG:H@50oC)→285.1 (FLG:H@100oC)→284.9 eV (FLG:H@200oC)] as clearly shown in the first order differential spectrum as an inset below of Figure 3. This change in the absorption edge is attributed to the change in the band gap of FLG:H@100-200oC due to the structural rearrangement via hydrogen attachment.34 A very low intense peak is also observed at ~283.3 eV, nearly 2.0 eV lower than the π* state for the FLG:H@50oC [As shown in (Figure S1 (c) in supporting information]. While this feature has been observed in graphene samples in the past, the origin of it is still highly debated. Hou et al. and Entani et al. have considered that this peak originates from the zig-zag edge C atoms which have a spin-polarized edge state closed to the Fermi level.34,35 They have proposed that there is a difference in the 1s core level binding energy between the carbon atom located in the interior of the graphene nano-cluster and one located at the zig-zag edge34 Alternatively, Pacile et al have ascribed this shoulder to the splitting of the π* bands in graphene.36 In the theoretical work by Hua et al, this shoulder has been ascribed to a special extended final state or to Stone-Wales defects.37 As reported by Hou et al., the intensity and the position of this peak strictly depends on hydrogen content as well as the ratio of monohydrogen (-CH) to dihydrogen (-CH2) terminations in the graphene structure.35 While monohydrogen termination produces the shoulder at approximately 2-2.5 eV lowers to the π* resonance, mono-hydrogen termination is stable only at very low hydrogen partial pressures. Under “standard” condtions, the structures are more likely to be a mixture of mono and dihydrogen terminations along the graphene edges.35 For our samples, in the case of FLG:H@100oC (200oC) samples the π* peak lying 0.2eV (0.4 eV) below with compared to FLG:H@50 (inset below in Figure 3), leading to the conclusion that the dihydrogen (-CH2) termination is increasing with the increase in temperature treatment. It is also possible that the defects being created by the hydrogen plasma treatment. Raman shows an increase in the defects at 50oC with anomalous behavior at 100oC and 200oC.
Figure 3. XANES spectra of pristine and FLG:H samples. The top inset shows the increase in the C-H content whereas the bottom inset shows the first order differential spectrum for the scans (inset below: Green and Blue spectra is shifted ~0.2 eV).
Apart from π* and σ* resonance peaks, two other peaks at ~287.4 (±1) eV and ~288.5 (±1) eV (inset in top panel of Figure 3) are observed and ascribed as signature of C-H bonds and interlayer graphite states, respectively. When compared to pristine FLGs, the FLG:H spectra shows an increased intensity of the C-H peak accompanied by a reduction in the interlayer graphite peak intensity. This increase in the C-H peak intensity confirms the formation of sp3-rich structures having a higher content of C-H bonds. We have estimated the C-H content relative to pristine FLG from the C-H peak in C K-edge XANES spectra using a proper baseline corrected curve-fitting procedure (in the range of 287-291 eV), is shown in Figure 4. In this figure the peak with green shaded areas are the contributions of C-H bond. Other two peaks are the contribution of inter-layer graphite states. It is observed that C-H contents of FLG:H are significantly decreases (0.065→0.032→0.019) (arbitrary unit) with increase of hydrogen functionalization temperatures (50oC→100oC→200oC). During the functionalization, process all conditions were remains unchanged except the temperature during hydrogen plasma and it shows that the C-H bonds. It is known that with the decrease in the hydrogen content the band gap of graphene reduces.38 However, in our case it is estimated that the band gap actually increases slightly for FLG:H@100oC/200oC when compared to pristine FLGs and FLG@H:50oC. This can be observed via the shift of C K-edge towards lower energy levels with the reduction of C-H content (see Figure 3, inset below). However, we have trying to find the bandgap with the help of C Kα x-ray emission spectra (XES) and C K-edge XANES spectra39 as shown and described with Figure 5. It was observed that the extrapolation of the leading edges of XES and XANES spectra leads to an clear intersection, implying that FLG and FLG:H have a “zero” band gap, similar to the metallic highly oriented pyrolytic graphite (HOPG). While, one would expect that the formation of sp3 configuration will lead to a change in the band gap such as in graphane (band gap of 3.12 eV). Graphane is a direct gap material for which both electron and optical gaps are the same, however most of the partially hydrogenated systems demonstrate indirect optical band gap.40 It should be noted that XANES, measured in electron yield mode is a surface sensitive technique with the electron escape depth of ~3-5 nm.33 As mentioned before, the shift in the absorption edge of the C K-edge spectra leads us to the conclusion that the band gap increases for the FLG:H@100oC-200oC as compared to pristine FLGs and FLG:H@50oC. This observation also observed in XPS measurements as shown in Figure 6. In this figure the carbon C (1s) XPS spectrum of the FLG and FLG:H shows a peak at 284.65 eV for sp2 hybridized carbon atoms. This value is comparable to the C (1s) binding energy in graphite (284.5 eV). After bonding with hydrogen this peak is shifted ~0.15 eV to higher binding energy (Figure 6b) for the FLG:H@100oC (200oC) suggesting the bang gap slightly changes with hydrogenation of graphene. In addition one shoulder is observed at ~284.4 eV for the FLG:H@50oC that assigned as the peak for “zigzag” state of graphene and is similar to a very week peak that we observed at ~283.5 eV in XANES spectra [as shown in Figure S1 (c) in the supporting information]. Hence, it is important to consider the effect of temperature on the formation and distribution of C-H bonds. It is quite interesting to observe that the estimated C-H contents are approximately 3:1.5:1 (≅ 6:3:2) ratio at 50oC, 100oC and 200oC respectively, indicating the C-H bonds are distributed at three different ways at three different temperatures on graphene surface. At relatively lower temperatures of 50oC, we can consider the possibility of hydrogenation occurring on only “top-most surface layer” of the FLGs.41 At higher temperatures (100oC-200oC), we believe that hydrogen can be passivate the surface as well as form C-H bonds in the “inner-layers of FLGs”, which may not be detected by XANES due to the electron escape depth limitation. The hydrogenation can occur in the inter-layer of FLGs only after overcoming the energy barrier to penetrate the centre of the hexagonal carbon in the top-most surface layer.42
Figure 4. XANES Fitting curve for the estimation of C-H content.
Figure 5. Band gap determination from normalized C K-edge XAS and K XES spectra of FLG and FLG:H.
Figure 6. Magnetic hysteresis loops obtained for FLG and FLG:H samples at 300K and 40K, respectively.
Hence, the C-H contents observed and measured in the XANES spectra are lower at 100oC-200oC temperatures. Under the same hydrogenation conditions except temperature, the different hydrogen coverage on first layer and second layer indicates the corresponding hydrogenation barriers differ from each other. Based on this, hydrogenation and C-H bond formation in FLG at different functionalization temperatures; we may consider the formation of graphene supported graphone/graphane bi- or tri-layer nanostructure materials. Again, Raman spectra shows that the ID/IG ratio decreased for the H-functionalized FLG at 100-200oC temperature compared to FLG:H@50oC, indicating a slow de-hydrogenation process may also have occurred along with hydrogenation process in H2-plasma atmosphere. This could be another reason for the lower content of C-H bonds present in FLG:H functionalized at 100 and 200oC. Luo et al have observed that the dehydrogenation process starts at the temperatures of 75-100oC and can be completed at 350oC with long annealing duration, although in our case, the hydrogenation process is carried out for a 90 sec duration only.32 So, the effect of de-hydrogenation process should ideally be low, leading to the conclusion that at higher temperatures, the surface passivation is followed by the penetration of “top-most” graphene layer to form C-H bonding in the inter-layers of the FLGs. Based on the formation of this graphene supported graphone/graphane bi-/tri-layer nano-structure materials we have studied the magnetic behaviors of these materials.
3.4 Magnetic Behaviors (M-H loops) at 300 K and 40 K temperature
The magnetic properties of the FLGs and FLG:H samples were measured in the range of -2 kOe < H < 2 kOe at temperatures of 300 K and 40 K, respectively. The measured magnetic hysteresis loops are shown in Figure 7, with the FLG:H@50oC sample showing the best ferromagnetic behavior with maximum hysteretic features with saturation (Ms = 13.94 x 10-4 emu/gm), while other samples shows lower hysteretic features with saturation (see Table 1). As compared to pristine FLGs, the magnetic moment values FLG:H@100oC & FLG:H@200oC [as shown in Figure S1(a, b) in the supporting information] are slightly higher due to hydrogen incorporation in the FLG resulting in the formation of sp3 hybridized carbon structure through mono- and/or di-hydrogen termination. Since, the FLG samples are free from any catalyst/magnetic impurities (mot shown), the observed magnetism in the samples can be attributed to (i) defects and vacancies created during synthesis, (ii) creation of sp3 hybridised structures.43-45 The ID/IG ratio trend of pristine and hydrogenated FLGs (Figure 2) shows that the FLG:H@50oC samples has the highest defect ratio along with the highest content of hydrogen as measured from XANES. Thus, the FLG:H@50oC samples are expected and indeed show the highest magnetization behaviour. As discussed before, at the relatively lower temperatures of 50oC, the hydrogenation may possibly occur on only the “top-most surface layer” of the FLGs; thereby favoring the higher observed magnetic moment.41 Similar to the results reported by others, we observed maxima in the magnetization at lower temperatures especially for FLG:H@50oC.46 Based on different hydrogen attachment on graphene [as shown in Figure S2 in the supporting information], Yazyey et al. predicted47 that the ortho-dimers and para-dimers are nonmagnetic; while single hydrogen attachment (monomer) to be magnetic.16 Probably this is the reason why FLG:H@50oC is more magnetic than FLG:H@100oC (200oC).
Figure 7. Temperature dependent of magnetization (M-T)
Table 1: Magnetization parameters of FLGs and FLGs:H
|
Sample |
MS (emu/gm x 10-4) |
HC (Oe) |
||
|
|
40K |
300K |
40K |
300K |
|
Pristine FLGs |
3.47 |
2.59 |
111.25 |
82.63 |
|
FLG:H@50C |
13.94 |
12.91 |
75.32 |
54.36 |
|
FLG:H@200C |
6.10 |
6.40 |
76.15 |
110.06 |
Since the magnetism observed in FLG:H is attributed to an intrinsic mechanism beyond reasonable doubt, it is important to discuss the role of hydrogen in enhancing the magnetism in nanostructured carbon and how it can be promoted during the synthesis itself. It has been shown theoretically that hydrogenation is an efficient way in which to introduce and enhance magnetism in graphene sheets. The addition of hydrogen leads to the rupturing of the delocalised p bonding network of graphene, leaving the 2pz electrons in the un-hydrogenated carbon atoms unpaired, and thereby extending the p-p interactions resulting in the long-range ferromagnetic coupling with a putative higher Curie temperature and a more homogeneous magnetism.48,49 Now, similar to the functionalisation strategies of other nanomaterials, the synthesis of hydrogenated graphene can be done via either a wet chemistry route or by plasma-based processes. The wet chemistry approach includes solution based Birch reduction of graphite oxide to yield graphane or by liquid phase hydrogenation/exfoliation of graphite.50,51 The plasma functionalization route involves hydrogenation of sp2 carbon materials such as CNTs, graphene or graphene oxide in a hydrogen gas/plasma environment.51 Arc-discharge of graphite in a hydrogen rich environment has also been shown as an effective method for the synthesis of graphane.52 However, theoretical calculations have suggested that the formation of graphene via hydrogenation of graphene will not yield large graphitic domains, since uncorrelated H frustrated domains are expected to be formed during the early stages of hydrogenation reaction.51. This will invariably lead to the shrinkage of the graphene sheet leading to extensive sheet corrugations; thus making the direct deposition of graphane more desirable.51 Zhou et al have proposed a physical method to fabricate a semi-hydrogenated graphene sheet.49 Their idea revolves around the use of graphane as a substrate to support the Boron nitride sheet, after which the BN sheet is fluorinated. As the binding of the F with N is highly unstable, the F-BN configuration can be easily achieved. Due to the presence of unpaired electrons, theNatoms are quite reactive in nature and upon the application of pressure, will pick up the H atoms from graphane. When the applied pressure is removed, the resultant structure is semi-hydrogenated in nature.49 In our case, since we are depositing FLG from the gas phase in plasma, the direct deposition of hydrogenated graphene via plasma deposition similar to work reported by Wang et al can be a feasible route for enhancing the magnetic properties of FLG during the synthesis itself.53 The process reported by Wang et al involves the use of remote discharged 13.5 MHz radiofrequency plasma inside an ultra-high vacuum source.53 The pre-cracking of the gaseous precursors to generate the reactive free radicals in gas phase allows for lower substrate temperatures and also limits the damage caused by energetic plasma ions during the growth of film. The growth process was carried out using a premixed 5% CH4 in H2, resulting in an excess of atomic hydrogen in the gas phase and the inevitable hydrogenation of graphene films with formation of graphane.53 In literature, the role of hydrogen during the non-catalytic growth of FLG has been linked to the etching of amorphous carbon films which may occur during the initial nucleation stages54,55. Thus, for the formation of magnetic graphene structures, careful tuning of plasma parameters such as gas conditions, plasma power, temperature, ion energy and bias in the microwave plasma will be required. The ferromagnetic order arises from the free spins available via the conversion of sp2 to sp3-hybridised structures and/or from the unpaired spin electron from the defects induced upon hydrogenation.56 Both these factors may in principle be responsible for producing fundamental magnetic species. The ferromagnetic ordering of the spins is energetically preferable for the AA distribution in the graphene plane. Therefore, it can be stated that the ferromagnetic exchange of spins of the localized states in graphane is possible only among the H-vacancy defects located on the exchange neighboring carbon atoms.57,58 Defects in our bi-/trilayer graphene break the translational symmetry of the lattice and create localized states at the Fermi energy to produce an effective self-doping, where charge is transferred from defects to the bulk. In the presence of local electron-electron interactions, these localized states become spin-polarized, leading to the formation of pseudo-local moments.59.Most of the theoretical45,60-62 and experimental60,61 works find that the net spin is stable within a large conjugation system in unit structures of graphene at room temperature and their stability is due to the huge p-conjugation in these molecules. If indeed the long-range orderly magnetic coupling of these spins may arise via either intra-molecular interaction in individual graphene sheets or intermolecular interaction between neighbouring graphene sheets, then stable ferromagnetism could arise.45
3.5 Temperature dependent Magnetization (M-T)
In Figure 7, we show the temperature-dependence of magnetization of FLG and FLG:H measured at 100 Oe. Figure 7 indicates clearly that the highest magnetization is for the FLG:H@50oC and lowest magnetization is for the FLG. In case of FLG:H@100oC/200oC, the magnetizations lower than FLG:H@50oC but higher than FLG. This change of magnetization is strictly depends on the content of hybridized hydrogen with carbon and formed C-H bonds and is consistence with the C-H content obtained from C K-edge XANES spectra.
Though the origin of ferromagnetism in carbon nanomaterials is not yet clear, various theoretical predictions and some experimental evidence have been offered recently to understand the underlying mechanism(s).63-65 Among them, proton irradiation experiments suggest that intrinsic carbon defects such as the lattice defects, vacancies, edges or topological defects and voids in the few-layer graphene give rise to localized magnetic states at the Fermi level, and the number of these states roughly scales with the defect perimeter.66 Defects in few-layer graphene break the translational symmetry of the lattice and create localized states at the Fermi energy to produce an effective self-doping, where charge is transferred to/from defects to the bulk. In the presence of local electron–electron interactions, these localized states become spin polarized, leading to the formation of local moments.6
3.6 Atomic Force Microscopy (AFM) and Magnetic Force Microscopy (MFM)
We agreed that the room-temperature ferromagnetism is an intrinsic property of graphene-based materials, and for direct and conclusive evidence, we have performed further magnetic force microscopy (MFM) analysis.
Low moment magnetic probes with Co/Cr coating were used to detect magnetic domains in the pristine and hydrogenated FLG samples. Figure 8 and Figure 9 shows topographic (height), amplitude and phase signals were imaged simultaneously for both tapping mode AFM (TM-AFM) and MFM to assess for correlation of surface features, identify and eliminate possible artifacts and to assess effects of magnetization. The magnetized Co/Cr coated probe interacts with magnetic field gradients generated by magnetic domains within the prepared samples resulting in changes in the phase and amplitude of the oscillating cantilever. Therefore, from the amplitude and phase images the existence of magnetic domains in the samples should be evident. The MFM phase and amplitude images show very good correlation in magnetic domain positions. For all samples, the magnetic domains appear as dark and bright-localized regions in phase and amplitude images respectively. Images clearly shows that the domains in the FLG:H are more localized than FLG. A simple scaling of MFM phase data suggests that the pristine FLGs may have the weakest magnetization, whereas the FLG@50oC may have the strongest magnetization, which is consistent with the M-H magnetization results, described above.
Figure 8. Atomic Force Microscopy images of pristine (a-c) and hydrogenated FLGs [(d-f) @ 50oC and (g-i) @200oC]
Figure 9. Magnetic Force Microscopy images of pristine (a-c) and hydrogenated FLGs [(d-f) @ 50oC and (g-i) @200oC].
4 Role of Hydrogen for the magnetism behaviour in Graphene: A theoretical idea
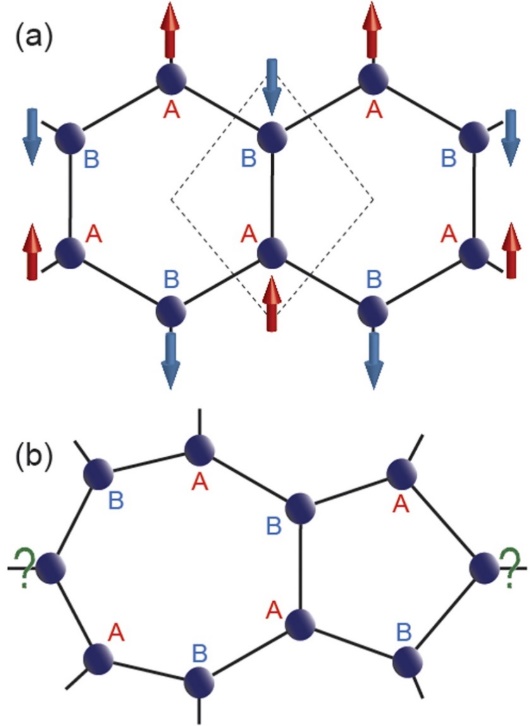
Graphene is a metal-free material and have no magnetic atoms. Its honeycomb structure is a bipartite lattice, which can be viewed as two interpenetrating hexagonal sublattices of carbon atoms say, A and B (see Figure 10a). The basic idea of magnetism in graphene lies in Lieb’s theorem for bipartite lattice.68 The bipartite nature of pristine graphene collapses at such defects and discrimination of NA and NB becomes impossible. That may lead to asymmetric distribution of up and down spins and may induce magnetism; or simply due to inequality between two sublattice points A and B (i.e., NA ≠ NB), magnetic moment is induced. In graphene, two sublattice points, A and B prefer opposite spin occupancies, making the overall net magnetization zero (see Figure 10a). Therefore, it is expected that, the vacancy defects can introduce inequality between NA and NB, making the two-dimensional graphene magnetic.69-76 The formation of zigzag edges, along a certain crystallographic direction of graphene can also introduce net magnetization, in spite of NA = NB.77-80 This magnetization in semi-infinite zigzag edge graphene can be attributed to the formation of peculiar edge localized states near Fermi energy and the spins tend to align parallelly on the same sublattice points along the same edge, giving rise to a long-range ferrimagnetic coupling.81-84. Formation of another parallel zigzag edge like geometry results in total zero magnetization by putting the spins in opposite polarization on the other sublattice points along the opposite edge. Moreover, introduction of holes can induce net magnetization in zigzag edge graphene.85-87 Another origin of the magnetism in graphene, are unusual bonding and hybridization. This is owing to the catenation property of carbon, which allows diverse hybridization possibilities. The growth of wafer scale graphene within CVD technique often results in several kinds of defects like point defects (PDs), due to non-periodic nature and grain boundaries (GBs), due to periodic nature among pristine graphene domains with different crystallographic orientations88-93 that significantly modify the electronic, magnetic and transport properties of graphene. Moreover, the bipartite phenomenon does not exist on these defects (see Figure 10b), giving rise to unusual magnetic properties known as defect-induced magnetism. The H-vacancy defects induced on one side of graphane plane (or substitution of H-atom on one side of graphene plane) and placed on the neighboring carbon atoms are found to be the source of ferromagnetism which is distinguished by the high stability of the state with a large spin number in comparison to that of the singlet state and is expected to persist even at room temperatures.94 Castro et al. found the ferromagnetic behaviour in bilayer graphene.95. Various reasons have been put forward for the formations of magnetic moments in graphene, such as, structural defects (See Figure 11, vacancies, substitutional atom, ad-atoms)96-98, existence of zigzag edges99,100, etc.
Figure 10. (a) The graphene lattice with rhombus unit cell (dashed box) consisting of two distinct sublattice points, A and B that prefer to localize opposite spins, making the whole system antiferromagnetic with same number of A and B sublattice points, i.e., NA = NB. Note that, each A (B) sublattice point is connected to three B (A) sublattice points. (b) One commonly known defect in graphene, namely Stone-Well’s defect consisting of fused five and seven membered rings. The bipartite characteristic collapses in such defects due to undefined sublattice nature emphasized by the “?” marks, giving rise to unusual magnetic properties (Re-use with permission from Ref. 85).
4.1 Defects in graphene
Magnetism in graphene has been found to originate from various defects, e.g., vacancy, edge formation, add-atoms etc. Defects in ideal graphene can be introduced by both vacancies and external doping. Many experimental works have reported the existence of magnetism in carbon materials by electrons or ions irradiation.101-103. The common feature of these defects is that carbon atoms are removed from the graphene sheet, which gives quasi-localized states at the Fermi level.104,105 A number of defects are possible in graphene. The graphene with defect shows magnetism and are depends upon the type and concentration of defects. In the following, different types of defects induced magnetization of graphene are discussed in detail.
4.2. Ad-atoms-Defects-induced magnetism in graphene
Defects by adsorptions of atom or molecule can produce magnetism and hence magnetic moments. Yazyev et al.69 and Boukhvalov et al.106 have studied the adsorption of H-atoms on graphene. Their results confirmed that such adsorption will lead to magnetic moments on neighboring carbon atoms and such spin-polarized states are mainly localized around the adsorptive hydrogen. Another feature is that the sp2 hybridized carbon atoms will become sp3 hybridized carbon on H-atoms that makes the graphene to lose the D3h symmetry. Boukhvalov et al.106 also investigated the magnetic coupling under hydrogen pair. The results show that only the H-atoms distributing on the same sublattices can introduce ferromagnetic coupling, while on the nearest carbon pairs, the dangling bonds of carbon atoms are saturated, leading to non-magnetic system. Other possible adsorptive atoms include carbon107, nitrogen108, oxygen107 and boron atoms. There are different possible structures for ad-atom defects in graphene108-110 and the adsorptive carbon, nitrogen, and oxygen atoms prefer the bridge-like positions on graphene surface. Carbon and nitrogen atoms induce magnetic moments in the graphene, while oxygen and boron atom cannot. The adsorption energies and bond lengths of defected graphene with different adatoms are different. The adsorption energy of a B-adatom is almost the same as that of N-adatom but smaller than that of a C-adatom. The ad-atom defects distort the graphene structure perpendicular to the plane of the graphene structure near the defect as shown Figure 11(d) and Figure 12. It was observed by Singh and Kroll that the magnetic moment on C-adatom is 0.44 μB and N-adatom is 0.56 μB, while B-adatom and O-adatoms is zero. Thus, the graphene with C and N adatoms107,108 are magnetic, while B-adatoms and O-adatoms are non-magnetic.107 The magnetic moment due to C-adatoms on graphene has been explained by counting arguments that two of four valence electrons of the C-adatom participate in covalent bonding with the C-atoms in graphene, one electron goes to the sp2 dangling bond of the C-adatom and the fourth one is shared between the sp2 dangling bond and the pz orbital of the adatom108,110 The pz orbital of the C-adatom is orthogonal to the π orbitals of graphene and cannot make any bands. Consequently, the pz orbital remains localized and spin polarized. Thus, the half electron shared by the pz orbital gives rise to a magnetic moment. The magnetic moment induced due to an adatom also depends upon the coupling between the π orbitals of graphene and the p orbitals of the adatom.110 In the N-adatom two valence electrons are involved in making covalent bonds with the C atoms of graphene, two electrons form a lone pair and the remaining fifth electron in the pz orbital gives rise to a magnetic moment; which is slightly higher than that due to the C-adatom. Due to the repulsion from the lone pair, the pz orbital of the N-adatom is not completely orthogonal to the π orbitals of graphene and forms a polarized band near the Fermi level. This partially filled band gives rise to a fractional magnetic moment. However, in the B-ad-atom two valence electrons are involved in covalent bonding with C atoms of graphene and a third electron is in the s orbital of the ad-atom which is not orthogonal to the π orbitals of graphene and forms bands with them. Consequently, B-ad-atoms do not induce any magnetism in graphene. The magnetic moments induced due to C and N adatoms are independent of ad-atom defect concentration because the magnetic moment due to C and N ad-atoms depends mainly upon the coupling between the π electrons and pz unpaired electrons of ad-atoms. This coupling is independent of the ad-atom-defect concentration.
Figure 11. (a) ideal graphene, (b) graphene with one atom vacancy, (c) graphene with one substitutional atom and (d) graphene with one ad-atom defect [Re-use with permission from Ref 97]. .
Figure 12. The ad-atom distorts the graphene structure perpendicular to the plane of the graphene (Re-use with permission from Ref 97).
4.3 Substitutional-Atom-induced magnetism in graphene
The substitutional B and N atoms are sp2 hybridized like the C atoms in a graphitic network. If N atom dopant does not occupy the substitutional sp2 site in a graphitic network, it is adsorbed on the surface of the graphitic network.111,112 The N atom contributes two electrons, while the B atom contributes no electron to the π-electron system of C atoms. The substitutional atom and vacancy defects in graphene break the symmetry in the π-electron system of C atoms in graphene. This symmetry breaking gives rise to the magnetic quasi-localized states in graphene.69,113 The B and N substitutional atoms induce magnetism in graphene depending upon the defect density concentration. The magnetism induced due to substitutional atoms in graphene can be understood due to the fact that a donor (acceptor) atom forms a narrow band above the Fermi level.114,115 In this case, N is the donor atom; whereas B is the acceptor atom. When the defect density is low enough the charge transfer from defect bands to π bands is complete and no magnetism is induced in graphene. However, when defect density reaches a critical density the Fermi level reaches the defect band resulting in a high density of defect states at the Fermi level. According to the Stoner criteria this leads to the development of a net magnetic moment in graphene.116 The local magnetic moments having strong long range magnetic coupling are responsible for the high-temperature magnetism observed in carbon-based materials.117 The induced magnetic moment could be explained by the fact that the substitutional doping of a B or N atom for a C atom in graphene breaks the symmetry between A and B sublattices. When a substitutional defect is created in an α sublattice the π electron in the pz orbital of the corresponding C atom in the B sublattice is shared between the defect state of the substitutional atom and the pz orbital of the C atom of the B sublattice. The half electron shared by the defect state gives to a magnetic moment. The substitutional defects are planar in the sense that there is in-plane displacement of C atoms near the substitutional defect.
4.4 Vacancy-induced magnetism in graphene
Vacancy-induced magnetism in graphene depends upon the magnetic textures associated with removing a single atom (vacancy) and multiple adjacent atoms (voids) as well as the magnetic interactions between them. The vacancy defects in graphene break the symmetry in the π-electron system of C atoms in graphene. This symmetry breaking gives rise to the magnetic quasi-localized states in graphene.69,113 As the symmetry between sublattice (A and B) is locally violated near the vacancy, the magnetic moment is induced around it. The magnetic moment per defect induced in graphene due to a vacancy and is depend upon the defect concentration and packing geometry of defects. On removal of one C atom, each of the three neighbouring C atoms has one sp2 dangling bond. Upon relaxation the vacancy defect undergoes Jahn-Teller distortion where the neighbour atoms to the vacancy site undergo a displacement and form weak bonds.118,119 The displacement of C atoms and the formation of weak bonds after the relaxation of a vacancy defect created in graphene. The local three fold symmetry breaks down due to the Jahn-Teller distortion induced by reconstruction of the dangling bonds left after removing one C atom. This gives rise to the in-plane displacement of other C atoms near the vacancy site in the graphene lattice. The vacancy defect induced magnetism in graphene depends upon the possibility of covalent bonding in C atoms near the vacancy site. Again, the displacement of C atoms and formation of pentagons is due to the formation of weak bonds near the vacancy site. The formation of pentagons partially saturates the three dangling bonds, but the remaining unsaturated bond is responsible to the fractional local magnetic moment near the vacancy site. The formation of extra bonds near the vacancy site gives rise to a reduced magnetic moment. A magnetic moment of 1.15 μB has been predicted for the closest packing of vacancy defects69 in a graphene sheet. Lehtinen et al.110 have predicted a magnetic moment of 1.04 μB for the ground state of vacancies in a graphite sheet.
However, in the vacancy defect, the total magnetic moment is determined by the contribution of localized sp2 dangling bond states and extended quasi-localized defect states (localized pz orbitals). Magnetism in carbon systems due to vacancies depends strongly on their concentration as well as the local bonding environment.120 The magnetization decreases monotonically120 with increasing vacancy density and are depends upon the packing geometry of defects. The dependence of magnetism due to vacancy defects on the concentration and packing geometry is due to the difference in the structural changes induced by the relaxation of vacancy defects in graphene. Singh and Kroll mentioned that the Ruderman-Kittel-Kasuya-Yosida (RKKY)-type interactions between the local magnetic moments induced at the vacancy sites are also responsible for this dependence because the RKKY interactions decay as r-3 (where r is the distance between the defects).121 According to the Stoner picture the magnetic ordering is driven by the exchange energy which depends upon the pz orbitals of carbon atoms. Ferromagnetic ordering is the only possibility for the magnetism originating from the quasi-localized states induced by defects in the same sublattice because of the non-oscillating behavior of magnetization within the same sublattice and indirect RKKY interaction due to the semi-metallic properties of graphene.121
4.5 Hydrogen Vacancy in graphene
Hydrogen vacancies in graphane are products of incomplete hydrogenation of graphene. The missing H atoms can alter the electronic structure of graphane and therefore tune the electronic, magnetic, and optical properties of the composite.122 A variety of well-separated clusters of hydrogen vacancies in graphane is possible that includes the geometrical shapes of triangles, parallelograms, hexagons and rectangles. The energy levels caused the missing H and are generated in the broad band gap of pure graphane. All triangular clusters of H vacancies are magnetic, the larger the triangle the higher the magnetic moment. The defect levels introduced by the missing H in triangular and parallelogram clusters are spin-polarized and can find application in optical transition. Parallelograms and open-ended rectangles are antiferromagnetic and can be used for nanoscale registration of digital information.
4.6 Grain boundary defects induced magnetism in graphene
Grain boundary is another route of achieving the magnetism in graphene.123-130 During deposition of graphene, several graphene nucleation centers grow independently and face themselves with unusual bonding environment, giving rise to the formation of grain boundaries. The origins of magnetism in such grain boundaries are letting of two nucleation centers interact with each other at their interface. The formation of unprecedented point defect, consisting of fused three-membered and larger carbon rings, which induces net magnetization to graphene. In case of periodic lattices, the appearance of array of point defects leads to the formation of magnetic grain boundaries. The net magnetization on these defects arises due to the deviation from bipartite characteristics of pristine graphene. The magnetic grain boundary induced dispersion less flat bands near Fermi energy, showing higher localization of electrons. These flat bands can be accessed via small doping, leading to enhanced magnetism. Moreover, the grain boundaries can induce asymmetric spin conduction behaviour along the cross boundary direction. These properties can be exploited for sensor and spin-filtering applications. The grain boundary dislocation with the core consisting of pentagon, octagon, and heptagon (5-8-7 defect) is a typical structural element of dangling bond GB (DBGB) with relatively low energies. Akhukov et al.131. studied by density functional calculations and found that the 5-8-7 defects are the carrier of the magnetic moments and their magnetic moment survives on hydrogenation. These confirm that the generic GB should contain magnetic moments that are robust enough, in particular, with respect to hydrogenation. Since GB in graphene is one dimensional object and cannot lead to magnetic ordering at any finite temperature.
4.7 Domain boundaries defects induced Magnetism in graphene
During the mass-scale production of graphene inevitably lead to a polycrystalline material, containing grain boundaries (GB)123 and recent theoretical prediction124 and experimental realization of domain boundaries (DB) in graphene by controlled deposition of the material on metallic substrates125 is established. In the case of GB’s, a large volume of works has accumulated in the last few years126-128, while for the DB produced in Lahiri et al. experiment, valley-filter properties129 and its effects on the magnetic edge states of a graphene ribbon130 have been theoretically investigated. The DB defect introduces a sharp resonance in the density of states (DOS) of graphene that lies just above the Fermi level in the neutral system, and is associated to electronic states that are very strongly confined to the core of the defect. When a graphene, containing a DB is doped and these quasi-1D states are populated, a ferromagnetic state is realized, which is confined to zigzag chains along the defect core that are fully immersed within a bulk graphene matrix. The electronic states introduced by GB in graphene are only partially confined to the defect core, while a DB introduces unoccupied electronic states near the Fermi level that are very strongly confined to the core of the defect, and that, when populated by doping, display a ferromagnetic ground state in a 1D defect that is fully contained within the bulk matrix and that consists entirely of carbon atoms. Being fully bulk-immersed, this ferromagnetic state is protected from reconstruction and should be more easily detectable experimentally than those predicted to exist along the edges of graphene.
4.8 Transition-Metal (TM)-atoms induced Magnetism in graphene
The atomic structure of TM atoms adsorbed on pristine and defected graphene, containing single and double vacancies (SV and DV). These TM-atoms strongly bind to the defected graphene, and that the hybridization of carbon sp2 and metal spd orbitals, combined with a different environment of the atom at SVs and DVs, gives rise to very peculiar magnetic properties of the atom-vacancy complexes.132 A metal atom adsorbed on SVs in a graphene sheet is associated with a substitutional impurity in graphene. This metal atoms form covalent bonds with the under-coordinated C atoms at the vacancy by breaking the weak C—C bond at the pentagon in the reconstructed vacancy.126,133 The TM atomic radii are larger than that of the carbon atom, the metal atoms displace outwards from the graphene surface, as reported earlier for Ni.134 The M@SV complexes are magnetic for M = V, Cr, and Mn, which have single-filled d states. The Fe and Ni impurities having double occupied states and an even number of electrons are nonmagnetic, while Co and Cu, having an odd number of electrons, are magnetic. The behaviours of M@DV complexes are magnetic for all TM from V to Co.
4.9 Topological defects induced magnetism in graphene
The extraordinary mechanical stiffness coexisting with ripples in graphene135 point toward topological defects as the main source of curvature.136,137 Nucleation of dislocations in the fabrication of the graphene by mechanical cleavage of graphite is practically unavoidable. These types of defects have been produced and observed with transmission electron microscopy in suspended graphene.138 This topological defect breaks the sublattice symmetry that involves uncoordinated atoms and induces localized magnetic moments in the lattice.
4.10 Spin-polarised states at Zig-Zag edges in graphene
Ferromagnetism, antiferro-magnetism and diamagnetism along with probable superconductivity exist in the graphene with irregular edges. There are two basic edge shapes are armchair and zigzag, which determine the magnetic properties of graphene. The presence of edges in graphene has strong implications for the low-energy spectrum of the π-electrons.77,78,79 The graphene with zigzag edges possess localized edge states with energies close to the Fermi level77-79,81; whereas this localized edge states are absent in armchair edges. Scanning tunnelling microscopy140-141 and high-resolution angle-resolved photoemission spectroscopy (ARPES)142 have provided evidence of edge-localized states. The presence of graphene edge states results in a relatively large contribution to the density of states (DOS) near the Fermi energy in a nanoscale system. These edge states play an important role in the magnetic properties of nanosized graphitic systems. Even weak electron-electron interactions make the edge states magnetic, and the ferrimagnetic spin alignment along the zigzag edge is favoured.78,81 The magnetic structures along the zigzag edges of graphene formed a chain of vacancies. The spin-orbit coupling tends to suppress the couple under-polarized ferrimagnetic order on the upper and lower edges, because of the open of the spin-orbit gap. As a result, in the case of the balance number of sublattices, it will suppress completely this kind of ferrimagnetic order. But, for the imbalance case, a ferrimagnetic order along both edges exists because additional zero modes will not be affected by the spin-orbit coupling.
5. Conclusion
In conclusion, room temperature ferromagnetism was observed in partially hydrogenated graphene. Hydrogenation was confirmed by XANES measurements with the appearance of a C-H stretching peak. The mechanism of the observed ferromagnetism is explained by the formation of unpaired electrons during the hydrogenation process, together with the remnant delocalized π-bonding network existing in the partially hydrogenated Graphene. The fabrication of a variety of spintronic devices requires room temperature ferromagnetic semiconductors. This hydrogenation process can easily turn graphene into a robust room-temperature ferromagnetic semiconductor and open up the possibility of making highly tunable graphene-based many important device applications, including spintronic nano-devices, magnetoresistance, magnetic memory devices, and so on.
Suppporting Information
The supporting Information is available at the FRT publications website at SI.
Notes
The authors declare no competing financial interest.
Acknowledgements
S.C.R. gratefully acknowledge the financial support received from the National Research Foundation (NRF), South Africa (Grant No. EQP13091742446).
References
[1] Novoselov KS. Electric Field Effect in Atomically Thin Carbon Films. Science 2004;306(5696):666–9. doi:10.1126/science.1102896
[2] Geim AK. Graphene: Status and Prospects. Science 2009;324(5934):1530–4. doi:10.1126/science.1158877
[3] Gass MH, Bangert U, Bleloch AL, Wang P, Nair RR, Geim AK. Free-standing graphene at atomic resolution. Nature Nanotechnology 2008;3(11):676–81. doi:10.1038/nnano.2008.280
[4] Stankovich S, Dikin DA, Dommett GHB, Kohlhaas KM, Zimney EJ, Stach EA, et al. Graphene-based composite materials. Nature 2006;442(7100):282–6. doi:10.1038/nature04969
[5] Li L, Qin R, Li H, Yu L, Liu Q, Luo G, et al. Functionalized Graphene for High-Performance Two-Dimensional Spintronics Devices. ACS Nano 2011;5(4):2601–10. doi:10.1021/nn102492g
[6] Hong AJ, Song EB, Yu HS, Allen MJ, Kim J, Fowler JD, et al. Graphene Flash Memory. ACS Nano 2011;5(10):7812–7. doi:10.1021/nn201809k
[7] Sofo JO, Chaudhari AS, Barber GD. Graphane: A two-dimensional hydrocarbon. Physical Review B. 2007;75(15). doi:10.1103/physrevb.75.153401
[8] Elias DC. Control of Graphene’s Properties by Reversible Hydrogenation: Evidence for Graphane. Science 2009;323:610–3. doi:10.1126/science.1167130
[9] Zhou J, Wang Q, Sun Q, Chen XS, Kawazoe Y, Jena P. Ferromagnetism in Semihydrogenated Graphene Sheet. Nano Letters 2009;9(11):3867–70. doi:10.1021/nl9020733
[10] Bostwick A, McChesney JL, Emtsev KV, Seyller T, Horn K, Kevan SD, et al. Quasiparticle Transformation during a Metal-Insulator Transition in Graphene. Physical Review Letters 2009;103(5). doi:10.1103/physrevlett.103.056404
[11] Haberer D, Vyalikh DV, Taioli S, Dora B, Farjam M, Fink J, et al. Tunable Band Gap in Hydrogenated Quasi-Free-Standing Graphene. Nano Letters 2010;10(9):3360–6. doi:10.1021/nl101066m
[12] Guisinger NP, Rutter GM, Crain JN, First PN, Stroscio JA. Exposure of Epitaxial Graphene on SiC(0001) to Atomic Hydrogen. Nano Letters 2009;9(4):1462–6. doi:10.1021/nl803331q
[13] Balog R, Jørgensen B, Wells J, Lægsgaard E, Hofmann P, Besenbacher F, et al. Atomic Hydrogen Adsorbate Structures on Graphene. Journal of the American Chemical Society 2009;131(25):8744–5. doi:10.1021/ja902714h
[14] Zhou J, Wang Q, Sun Q, Jena P. Stability and electronic structure of bilayer graphone. Applied Physics Letters 2011;98(6):063108. doi:10.1063/1.3555431
[15] Balog R, Jørgensen B, Nilsson L, Andersen M, Rienks E, Bianchi M, et al. Bandgap opening in graphene induced by patterned hydrogen adsorption. Nature Materials 2010;9(4):315–9. doi:10.1038/nmat2710
[16] Xie L, Wang X, Lu J, Ni Z, Luo Z, Mao H, et al. Room temperature ferromagnetism in partially hydrogenated epitaxial graphene. Applied Physics Letters 2011;98(19):193113. doi:10.1063/1.3589970
[17] Schmidt MJ, Loss D. Edge states and enhanced spin-orbit interaction at graphene/graphane interfaces. Physical Review B 2010;81(16). doi:10.1103/physrevb.81.165439
[18] Soin N, Roy SS, O’Kane C, McLaughlin JAD, Lim TH, Hetherington CJD. Exploring the fundamental effects of deposition time on the microstructure of graphene nanoflakes by Raman scattering and X-ray diffraction. CrystEngComm 2011;13(1):312–8. doi:10.1039/c0ce00285b
[19] Soin N, Roy SS, Mitra SK, Thundat T, McLaughlin JA. Nanocrystalline ruthenium oxide dispersed Few Layered Graphene (FLG) nanoflakes as supercapacitor electrodes. Journal of Materials Chemistry 2012;22(30):14944. doi:10.1039/c2jm31226c
[20] Soin N, Sinha Roy S, Roy S, Hazra KS, Misra DS, Lim TH, et al. Enhanced and Stable Field Emission from in Situ Nitrogen-Doped Few-Layered Graphene Nanoflakes. The Journal of Physical Chemistry C 2011;115(13):5366–72. doi:10.1021/jp110476m
[21] Soin N, Roy SS, Sharma S, Thundat T, McLaughlin JA. Electrochemical and oxygen reduction properties of pristine and nitrogen-doped few layered graphene nanoflakes (FLGs). Journal of Solid State Electrochemistry. 2013;17(8):2139–49. doi:10.1007/s10008-013-2073-8
[22] Ray SC, Palnitkar U, Pao CW, Tsai HM, Pong WF, Lin I-N, et al. Field emission effects of nitrogenated carbon nanotubes on chlorination and oxidation. Journal of Applied Physics. 2008;104(6):063710. doi:10.1063/1.2981090
[23] Ferrari AC, Meyer JC, Scardaci V, Casiraghi C, Lazzeri M, Mauri F, et al. Raman Spectrum of Graphene and Graphene Layers. 2006;97(18). doi:10.1103/physrevlett.97.187401
[24] Ferrari AC. Raman spectroscopy of graphene and graphite: Disorder, electron–phonon coupling, doping and nonadiabatic effects. Solid State Communications. 2007;143(1-2):47–57. doi:10.1016/j.ssc.2007.03.052
[25] Tuinstra F, Koenig JL. Raman Spectrum of Graphite. The Journal of Chemical Physics. 1970;53(3):1126–30. doi:10.1063/1.1674108
[26] Ferrari AC, Robertson J. Interpretation of Raman spectra of disordered and amorphous carbon. Physical Review B. 2000;61(20):14095–107. doi:10.1103/physrevb.61.14095
[27] Wu W, Yu Q, Peng P, Liu Z, Bao J, Pei S-S. Control of thickness uniformity and grain size in graphene films for transparent conductive electrodes. Nanotechnology. 2011;23(3):035603. doi:10.1088/0957-4484/23/3/035603
[28] Wang Y ying, Ni Z hua, Yu T, Shen ZX, Wang H min, Wu Y hong, et al. Raman Studies of Monolayer Graphene: The Substrate Effect. The Journal of Physical Chemistry C. 2008;112(29):10637–40. doi:10.1021/jp8008404
[29] Ryu S, Han MY, Maultzsch J, Heinz TF, Kim P, Steigerwald ML, et al. Reversible Basal Plane Hydrogenation of Graphene. Nano Letters. 2008;8(12):4597–602. doi:10.1021/nl802940s
[30] Ryu S, Han MY, Maultzsch J, Heinz TF, Kim P, Steigerwald ML, et al. Reversible Basal Plane Hydrogenation of Graphene. Nano Letters. 2008;8(12):4597–602. doi:10.1021/nl802940s
[31] Xie L, Jiao L, Dai H. Selective Etching of Graphene Edges by Hydrogen Plasma. Journal of the American Chemical Society. 2010;132(42):14751–3. doi:10.1021/ja107071g
[32] Luo Z, Yu T, Kim K, Ni Z, You Y, Lim S, et al. Thickness-Dependent Reversible Hydrogenation of Graphene Layers. 2009;3(7):1781–8. doi:10.1021/nn900371t
[33] Stöhr J. NEXAFS Spectroscopy. Springer Series in Surface Sciences. 1992; doi:10.1007/978-3-662-02853-7
[34] Hou Z, Wang X, Ikeda T, Huang S-F, Terakura K, Boero M, et al. Effect of Hydrogen Termination on Carbon K-Edge X-ray Absorption Spectra of Nanographene. The Journal of Physical Chemistry C. 2011;115(13):5392–403. doi:10.1021/jp110879d
[35] Entani S, Ikeda S, Kiguchi M, Saiki K, Yoshikawa G, Nakai I, et al. Growth of nanographite on Pt(111) and its edge state. Applied Physics Letters. 2006;88(15):153126. doi:10.1063/1.2194867
[36] Pacilé D, Papagno M, Rodríguez AF, Grioni M, Papagno L, Girit ÇÖ, et al. Near-Edge X-Ray Absorption Fine-Structure Investigation of Graphene. Physical Review Letters. 2008;101(6). doi:10.1103/physrevlett.101.066806
[37] Hua W, Gao B, Li S, Ågren H, Luo Y. X-ray absorption spectra of graphene from first-principles simulations. Physical Review B. 2010;82(15). doi:10.1103/physrevb.82.155433
[38] Gao H, Wang L, Zhao J, Ding F, Lu J. Band Gap Tuning of Hydrogenated Graphene: H Coverage and Configuration Dependence. The Journal of Physical Chemistry C. 2011;115(8):3236–42. doi:10.1021/jp1094454
[39] Chiou JW, Ray SC, Peng SI, Chuang CH, Wang BY, Tsai HM, et al. Nitrogen-Functionalized Graphene Nanoflakes (GNFs:N): Tunable Photoluminescence and Electronic Structures. The Journal of Physical Chemistry C. 2012;116(30):16251–8. doi:10.1021/jp303465u
[40] Shkrebtii AI, Heritage E, McNelles P, Cabellos JL, Mendoza BS. Graphene and graphane functionalization with hydrogen: electronic and optical signatures. physica status solidi (c). 2012;9(6):1378–83. doi:10.1002/pssc.201100705
[41] Bunch JS, Verbridge SS, Alden JS, van der Zande AM, Parpia JM, Craighead HG, et al. Impermeable Atomic Membranes from Graphene Sheets. Nano Letters. 2008;8(8):2458–62. doi:10.1021/nl801457b
[42] Zhou YG, Zu XT, Gao F, Nie JL, Xiao HY. Adsorption of hydrogen on boron-doped graphene: A first-principles prediction. 2009;105(1):014309. doi:10.1063/1.3056380
[43] Matte HSSR, Subrahmanyam KS, Rao CNR. Novel Magnetic Properties of Graphene: Presence of Both Ferromagnetic and Antiferromagnetic Features and Other Aspects. The Journal of Physical Chemistry C. 2009;113(23):9982–5. doi:10.1021/jp903397u
[44] Yang H-X, Chshiev M, Boukhvalov DW, Waintal X, Roche S. Inducing and optimizing magnetism in graphene nanomeshes. Physical Review B. 2011;84(21). doi:10.1103/physrevb.84.214404
[45] Rout CS, Kumar A, Kumar N, Sundaresan A, Fisher TS. Room-temperature ferromagnetism in graphitic petal arrays. Nanoscale. 2011;3(3):900. doi:10.1039/c0nr00870b
[46] Ning G, Xu C, Hao L, Kazakova O, Fan Z, Wang H, et al. Ferromagnetism in nanomesh graphene. 2013;51:390–6. doi:10.1016/j.carbon.2012.08.072
[47] Yazyev OV, Helm L. Defect-induced magnetism in graphene. Physical Review B. 2007;75(12). doi:10.1103/physrevb.75.125408
[48] Zhou J, Wu MM, Zhou X, Sun Q. Tuning electronic and magnetic properties of graphene by surface modification. Applied Physics Letters. 2009;95(10):103108. doi:10.1063/1.3225154
[49] Zhou J, Sun Q. How to fabricate a semihydrogenated graphene sheet? A promising strategy explored. Applied Physics Letters. 2012;101(7):073114. doi:10.1063/1.4746756
[50] Eng AYS, Poh HL, Šaněk F, Maryško M, Matějková S, Sofer Z, et al. Searching for Magnetism in Hydrogenated Graphene: Using Highly Hydrogenated Graphene Prepared via Birch Reduction of Graphite Oxides. ACS Nano. 2013;7(7):5930–9. doi:10.1021/nn4016289
[51] Pumera M, Wong CHA. Graphane and hydrogenated graphene. Chemical Society Reviews. 2013;42(14):5987. doi:10.1039/c3cs60132c
[52] Subrahmanyam KS, Kumar P, Maitra U, Govindaraj A, Hembram KPSS, Waghmare UV, et al. Chemical storage of hydrogen in few-layer graphene. Proceedings of the National Academy of Sciences. 2011;108(7):2674–7. doi:10.1073/pnas.1019542108
[53] Wang Y, Xu X, Lu J, Lin M, Bao Q, Özyilmaz B, et al. Toward High Throughput Interconvertible Graphane-to-Graphene Growth and Patterning. ACS Nano. 2010;4(10):6146–52. doi:10.1021/nn1017389
[54] Burgess JS, Matis BR, Robinson JT, Bulat FA, Keith Perkins F, Houston BH, et al. Tuning the electronic properties of graphene by hydrogenation in a plasma enhanced chemical vapor deposition reactor. Carbon. 2011;49(13):4420–6. doi:10.1016/j.carbon.2011.06.034
[55] Yuan GD, Zhang WJ, Yang Y, Tang YB, Li YQ, Wang JX, et al. Graphene sheets via microwave chemical vapor deposition. Chemical Physics Letters. 2009;467(4-6):361–4. doi:10.1016/j.cplett.2008.11.059
[56] Wang Y, Huang Y, Song Y, Zhang X, Ma Y, Liang J, et al. Room-Temperature Ferromagnetism of Graphene. Nano Letters. 2009;9(1):220–4. doi:10.1021/nl802810g
[57] Lee H, Son Y-W, Park N, Han S, Yu J. Magnetic ordering at the edges of graphitic fragments: Magnetic tail interactions between the edge-localized states. Physical Review B. 2005;72(17). doi:10.1103/physrevb.72.174431
[58] Berashevich J, Chakraborty T. Tunable band gap and magnetic ordering by adsorption of molecules on graphene. Physical Review B. 2009;80(3). doi:10.1103/physrevb.80.033404
[59] Lehtinen PO, Foster AS, Ma Y, Krasheninnikov AV, Nieminen RM. Irradiation-Induced Magnetism in Graphite: A Density Functional Study. Physical Review Letters. 2004;93(18). doi:10.1103/physrevlett.93.187202
[60] Harigaya K. The mechanism of magnetism in stacked nanographite: theoretical study. Journal of Physics: Condensed Matter. 2001;13(6):1295–302. doi:10.1088/0953-8984/13/6/309
[61] Esquinazi P, Spemann D, Höhne R, Setzer A, Han K-H, Butz T. Induced Magnetic Ordering by Proton Irradiation in Graphite. Physical Review Letters. 2003;91(22). doi:10.1103/physrevlett.91.227201
[62] Han K -h., Spemann D, Esquinazi P, Höhne R, Riede V, Butz T. Ferromagnetic Spots in Graphite Produced by Proton Irradiation. 2003;15(20):1719–22. doi:10.1002/adma.200305194
[63] Otani M, Takagi Y, Koshino M, Okada S. Phase control of magnetic state of graphite thin films by electric field. Applied Physics Letters. 2010;96(24):242504. doi:10.1063/1.3455069
[64] Sheng W, Ning ZY, Yang ZQ, Guo H. Magnetism and perfect spin filtering effect in graphene nanoflakes. Nanotechnology. 2010;21(38):385201. doi:10.1088/0957-4484/21/38/385201
[65] Ma T, Hu F, Huang Z, Lin H-Q. Controllability of ferromagnetism in graphene. Applied Physics Letters. 2010;97(11):112504. doi:10.1063/1.3485059
[66] Ohldag H, Tyliszczak T, Höhne R, Spemann D, Esquinazi P, Ungureanu M, et al. π-Electron Ferromagnetism in Metal-Free Carbon Probed by Soft X-Ray Dichroism. Physical Review Letters. 2007;98(18). doi:10.1103/physrevlett.98.187204
[67] Lehtinen PO, Foster AS, Ma Y, Krasheninnikov AV, Nieminen RM. Irradiation-Induced Magnetism in Graphite: A Density Functional Study. Physical Review Letters. 2004;93(18). doi:10.1103/physrevlett.93.187202
[68] Lieb EH. Two theorems on the Hubbard model. Physical Review Letters. 1989;62(10):1201–4. doi:10.1103/physrevlett.62.1201
[69] Yazyev OV, Helm L. Defect-induced magnetism in graphene. Physical Review B. 2007;75(12). doi:10.1103/physrevb.75.125408
[70] Nair RR, Sepioni M, Tsai I-L, Lehtinen O, Keinonen J, Krasheninnikov AV, et al. Spin-half paramagnetism in graphene induced by point defects. Nature Physics. 2012;8(3):199–202. doi:10.1038/nphys2183
[71] Deng H-Y, Wakabayashi K. Edge effect on a vacancy state in semi-infinite graphene. Physical Review B. 2014;90(11). doi:10.1103/physrevb.90.115413
[72] Yazyev OV. Emergence of magnetism in graphene materials and nanostructures. Reports on Progress in Physics. 2010;73(5):056501. doi:10.1088/0034-4885/73/5/056501
[73] Ma Y, Lehtinen PO, Foster AS, Nieminen RM. Magnetic properties of vacancies in graphene and single-walled carbon nanotubes. New Journal of Physics. 2004;6:68–68. doi:10.1088/1367-2630/6/1/068
[74] Hashimoto A, Suenaga K, Gloter A, Urita K, Iijima S. Direct evidence for atomic defects in graphene layers. Nature. 2004;430(7002):870–3. doi:10.1038/nature02817
[75] Fujii S, Enoki T. Clar’s Aromatic Sextet and π-Electron Distribution in Nanographene. Angewandte Chemie International Edition. 2012;51(29):7236–41. doi:10.1002/anie.201202560
[76] Ziatdinov M, Fujii S, Kusakabe K, Kiguchi M, Mori T, Enoki T. Direct imaging of monovacancy-hydrogen complexes in a single graphitic layer. Physical Review B. 2014;89(15). doi:10.1103/physrevb.89.155405
[77] Nakada K, Fujita M, Dresselhaus G, Dresselhaus MS. Edge state in graphene ribbons: Nanometer size effect and edge shape dependence. Physical Review B. 1996;54(24):17954–61. doi:10.1103/physrevb.54.17954
[78] Fujita M, Wakabayashi K, Nakada K, Kusakabe K. Peculiar Localized State at Zigzag Graphite Edge. Journal of the Physical Society of Japan. 1996;65(7):1920–3. doi:10.1143/jpsj.65.1920
[79] Wakabayashi K, Fujita M, Ajiki H, Sigrist M. Electronic and magnetic properties of nanographite ribbons. Physical Review B. 1999;59(12):8271–82. doi:10.1103/physrevb.59.8271
[80] Adams DJ, Gröning O, Pignedoli CA, Ruffieux P, Fasel R, Passerone D. Stable ferromagnetism and doping-induced half-metallicity in asymmetric graphene nanoribbons. Physical Review B. 2012;85(24). doi:10.1103/physrevb.85.245405
[81] Wakabayashi K, Sigrist M, Fujita M. Spin Wave Mode of Edge-Localized Magnetic States in Nanographite Zigzag Ribbons. Journal of the Physical Society of Japan. 1998;67(6):2089–93. doi:10.1143/jpsj.67.2089
[82] Wakabayashi K, Sasaki K, Nakanishi T, Enoki T. Electronic states of graphene nanoribbons and analytical solutions. Science and Technology of Advanced Materials. 2010;11(5):054504. doi:10.1088/1468-6996/11/5/054504
[83] Wakabayashi K, Dutta S. Nanoscale and edge effect on electronic properties of graphene. Solid State Communications. 2012;152(15):1420–30. doi:10.1016/j.ssc.2012.04.025
[84] Tao C, Jiao L, Yazyev OV, Chen Y-C, Feng J, Zhang X, et al. Spatially resolving edge states of chiral graphene nanoribbons. Nature Physics. 2011;7(8):616–20. doi:10.1038/nphys1991
[85] Dutta S, Wakabayashi K. Tuning Charge and Spin Excitations in Zigzag Edge Nanographene Ribbons. Scientific Reports. 2012;2(1). doi:10.1038/srep00519
[86] Dutta S, Pati SK. Novel properties of graphene nanoribbons: a review. 2010;20(38):8207. doi:10.1039/c0jm00261e
[87] Baringhaus J, Edler F, Tegenkamp C. Edge-states in graphene nanoribbons: a combined spectroscopy and transport study. Journal of Physics: Condensed Matter. 2013;25(39):392001. doi:10.1088/0953-8984/25/39/392001
[88] T N’Diaye A, Engler M, Busse C, Wall D, Buckanie N, Meyer zu Heringdorf F-J, et al. Growth of graphene on Ir(111). New Journal of Physics. 2009;11(2):023006. doi:10.1088/1367-2630/11/2/023006
[89] Geng D, Wu B, Guo Y, Huang L, Xue Y, Chen J, et al. Uniform hexagonal graphene flakes and films grown on liquid copper surface. Proceedings of the National Academy of Sciences. 2012;109(21):7992–6. doi:10.1073/pnas.1200339109
[90] Kotakoski J, Krasheninnikov AV, Kaiser U, Meyer JC. From Point Defects in Graphene to Two-Dimensional Amorphous Carbon. Physical Review Letters. 2011;106(10). doi:10.1103/physrevlett.106.105505
[91] Lahiri J, Lin Y, Bozkurt P, Oleynik II, Batzill M. An extended defect in graphene as a metallic wire. Nature Nanotechnology. 2010;5(5):326–9. doi:10.1038/nnano.2010.53
[92] Huang PY, Ruiz-Vargas CS, van der Zande AM, Whitney WS, Levendorf MP, Kevek JW, et al. Grains and grain boundaries in single-layer graphene atomic patchwork quilts. Nature. 2011;469(7330):389–92. doi:10.1038/nature09718
[93] Biró LP, Lambin P. Grain boundaries in graphene grown by chemical vapor deposition. New Journal of Physics. 2013;15(3):035024. doi:10.1088/1367-2630/15/3/035024
[94] Berashevich J, Chakraborty T. Sustained ferromagnetism induced by H-vacancies in graphane. Nanotechnology. 2010;21(35):355201. doi:10.1088/0957-4484/21/35/355201
[95] Castro EV, Peres NMR, Stauber T, Silva NAP. Low-Density Ferromagnetism in Biased Bilayer Graphene. Physical Review Letters. 2008;100(18). doi:10.1103/physrevlett.100.186803
[96] Nelayev VV, Mironchik PS. Construction of nano-objects and molecular dynamics simulation. Melker AI, editor. 2004; doi:10.1117/12.555441
[97] Singh R, Kroll P. Magnetism in graphene due to single-atom defects: dependence on the concentration and packing geometry of defects. Journal of Physics: Condensed Matter. 2009;21(19):196002. doi:10.1088/0953-8984/21/19/196002
[98] Muñoz-Rojas F, Fernández-Rossier J, Brey L, Palacios JJ. Performance limits of graphene-ribbon field-effect transistors. Physical Review B. 2008;77(4). doi:10.1103/physrevb.77.045301
[99] Kumazaki H, S. Hirashima D. Local Magnetic Moment Formation on Edges of Graphene. Journal of the Physical Society of Japan. 2008;77(4):044705. doi:10.1143/jpsj.77.044705
[100] Bhowmick S, Shenoy VB. Edge state magnetism of single layer graphene nanostructures. The Journal of Chemical Physics. 2008;128(24):244717. doi:10.1063/1.2943678
[101] Carbon Based Magnetism. Elsevier; 2006; doi:10.1016/b978-0-444-51947-4.x5000-2
[102] Esquinazi P, Spemann D, Höhne R, Setzer A, Han K-H, Butz T. Induced Magnetic Ordering by Proton Irradiation in Graphite. Physical Review Letters. 2003;91(22). doi:10.1103/physrevlett.91.227201
[103] Fujita M, Wakabayashi K, Nakada K, Kusakabe K. Peculiar Localized State at Zigzag Graphite Edge. Journal of the Physical Society of Japan. 1996;65(7):1920–3. doi:10.1143/jpsj.65.1920
[104] Shibayama Y, Sato H, Enoki T, Endo M. Disordered Magnetism at the Metal-Insulator Threshold in Nano-Graphite-Based Carbon Materials. Physical Review Letters. 2000;84(8):1744–7. doi:10.1103/physrevlett.84.1744
[105] Khveshchenko DV. Ghost Excitonic Insulator Transition in Layered Graphite. Physical Review Letters. 2001;87(24). doi:10.1103/physrevlett.87.246802
[106] Boukhvalov DW, Katsnelson MI, Lichtenstein AI. Hydrogen on graphene: Electronic structure, total energy, structural distortions and magnetism from first-principles calculations. Physical Review B. 2008;77(3). doi:10.1103/physrevb.77.035427
[107] Ma Y, Foster AS, Krasheninnikov AV, Nieminen RM. Nitrogen in graphite and carbon nanotubes: Magnetism and mobility. Physical Review B. 2005;72(20). doi:10.1103/physrevb.72.205416
[108] Sorescu DC, Jordan KD, Avouris P. Theoretical Study of Oxygen Adsorption on Graphite and the (8,0) Single-walled Carbon Nanotube. The Journal of Physical Chemistry B. 2001;105(45):11227–32. doi:10.1021/jp0122979
[109] Li L, Reich S, Robertson J. Defect energies of graphite: Density-functional calculations. Physical Review B. American Physical Society (APS); 2005 Nov 30;72(18). doi:10.1103/physrevb.72.184109
[110] Lehtinen PO, Foster AS, Ma Y, Krasheninnikov AV, Nieminen RM. Irradiation-Induced Magnetism in Graphite: A Density Functional Study. Physical Review Letters. 2004;93(18). doi:10.1103/physrevlett.93.187202
[111] Droppa R, Ribeiro CTM, Zanatta AR, dos Santos MC, Alvarez F. Comprehensive spectroscopic study of nitrogenated carbon nanotubes. Physical Review B. 2004;69(4). doi:10.1103/physrevb.69.045405
[112] Zhao M, Xia Y, Ma Y, Ying M, Liu X, Mei L. Exohedral and endohedral adsorption of nitrogen on the sidewall of single-walled carbon nanotubes. Physical Review B. 2002;66(15). doi:10.1103/physrevb.66.155403
[113] Kumazaki H, S. Hirashima D. Nonmagnetic-Defect-Induced Magnetism in Graphene. 2007;76(6):064713. doi:10.1143/jpsj.76.064713
[114] Carroll DL, Redlich P, Blase X, Charlier J-C, Curran S, Ajayan PM, et al. Effects of Nanodomain Formation on the Electronic Structure of Doped Carbon Nanotubes. Physical Review Letters. 1998;81(11):2332–5. doi:10.1103/physrevlett.81.2332
[115] Czerw R, Terrones M, Charlier J-C, Blase X, Foley B, Kamalakaran R, et al. Identification of Electron Donor States in N-Doped Carbon Nanotubes. Nano Letters. 2001;1(9):457–60. doi:10.1021/nl015549q
[116] P. Mohan. Magnetism in the Solid State. Solid-State Sciences. Springer-Verlag; 2006; doi:10.1007/3-540-30981-0
[117] Esquinazi P, Spemann D, Höhne R, Setzer A, Han K-H, Butz T. Induced Magnetic Ordering by Proton Irradiation in Graphite. Physical Review Letters. 2003;91(22). doi:10.1103/physrevlett.91.227201
[118] El-Barbary AA, Telling RH, Ewels CP, Heggie MI, Briddon PR. Structure and energetics of the vacancy in graphite. Physical Review B. 2003;68(14). doi:10.1103/physrevb.68.144107
[119] Telling RH, Ewels CP, El-Barbary AA, Heggie MI. Wigner defects bridge the graphite gap. Nature Materials. 2003;2(5):333–7. doi:10.1038/nmat876
[120] Zhang Y, Talapatra S, Kar S, Vajtai R, Nayak SK, Ajayan PM. First-Principles Study of Defect-Induced Magnetism in Carbon. Physical Review Letters. 2007;99(10). doi:10.1103/physrevlett.99.107201
[121] Vozmediano MAH, López-Sancho MP, Stauber T, Guinea F. Local defects and ferromagnetism in graphene layers. Physical Review B. 2005;72(15). doi:10.1103/physrevb.72.155121
[122] Ray SC, Soin N, Makgato T, Chuang CH, Pong WF, Roy SS, et al. Graphene Supported Graphone/Graphane Bilayer Nanostructure Material for Spintronics. Scientific Reports. 2014;4(1). doi:10.1038/srep03862
[123] Yu Q, Jauregui LA, Wu W, Colby R, Tian J, Su Z, et al. Control and characterization of individual grains and grain boundaries in graphene grown by chemical vapour deposition. Nature Materials. 2011;10(6):443–9. doi:10.1038/nmat3010
[124] Kahaly MU, Singh SP, Waghmare UV. Carbon Nanotubes with an Extended Line Defect. Small. 2008;4(12):2209–13. doi:10.1002/smll.200701039
[125] Lahiri J, Lin Y, Bozkurt P, Oleynik II, Batzill M. An extended defect in graphene as a metallic wire. Nature Nanotechnology. 2010;5(5):326–9. doi:10.1038/nnano.2010.53
[126] Simonis P, Goffaux C, Thiry P., Biro L., Lambin P, Meunier V. 2002;511(1-3):319–22. doi:10.1016/s0039-6028(02)01511-x
[127] Červenka J, Flipse CFJ. Structural and electronic properties of grain boundaries in graphite: Planes of periodically distributed point defects. Physical Review B. 2009;79(19). doi:10.1103/physrevb.79.195429
[128] Yazyev OV, Louie SG. Topological defects in graphene: Dislocations and grain boundaries. Physical Review B. 2010;81(19). doi:10.1103/physrevb.81.195420
[129] Gunlycke D, White CT. Graphene Valley Filter Using a Line Defect. Physical Review Letters. 2011;106(13). doi:10.1103/physrevlett.106.136806
[130] Lin X, Ni J. Half-metallicity in graphene nanoribbons with topological line defects. Physical Review B. 2011;84(7). doi:10.1103/physrevb.84.075461
[131] Akhukov MA, Fasolino A, Gornostyrev YN, Katsnelson MI. Dangling bonds and magnetism of grain boundaries in graphene. Physical Review B. 2012;85(11). doi:10.1103/physrevb.85.115407
[132] Krasheninnikov AV, Lehtinen PO, Foster AS, Pyykkö P, Nieminen RM. Embedding Transition-Metal Atoms in Graphene: Structure, Bonding, and Magnetism. Physical Review Letters. 2009;102(12). doi:10.1103/physrevlett.102.126807
[133] Lehtinen PO, Foster AS, Ma Y, Krasheninnikov AV, Nieminen RM. Irradiation-Induced Magnetism in Graphite: A Density Functional Study. Physical Review Letters. 2004;93(18). doi:10.1103/physrevlett.93.187202
[134] Banhart F, Charlier J-C, Ajayan PM. Dynamic Behavior of Nickel Atoms in Graphitic Networks. Physical Review Letters. 2000;84(4):686–9. doi:10.1103/physrevlett.84.686
[135] Booth TJ, Blake P, Nair RR, Jiang D, Hill EW, Bangert U, et al. Macroscopic Graphene Membranes and Their Extraordinary Stiffness. Nano Letters. 2008;8(8):2442–6. doi:10.1021/nl801412y
[136] Cortijo A, Vozmediano MAH. Electronic properties of curved graphene sheets. Europhysics Letters (EPL). 2007;77(4):47002. doi:10.1209/0295-5075/77/47002
[137] Cortijo A, Vozmediano MAH. Effects of topological defects and local curvature on the electronic properties of planar graphene. Nuclear Physics B. 2007;763(3):293–308. doi:10.1016/j.nuclphysb.2006.10.031
[138] Meyer JC, Kisielowski C, Erni R, Rossell MD, Crommie MF, Zettl A. Direct Imaging of Lattice Atoms and Topological Defects in Graphene Membranes. Nano Letters. 2008;8(11):3582–6. doi:10.1021/nl801386m
[139] Kobayashi Y, Fukui K, Enoki T, Kusakabe K, Kaburagi Y. Observation of zigzag and armchair edges of graphite using scanning tunneling microscopy and spectroscopy. Physical Review B. 2005;71(19). doi:10.1103/physrevb.71.193406
[140] Kobayashi Y, Fukui K, Enoki T, Kusakabe K. Edge state on hydrogen-terminated graphite edges investigated by scanning tunneling microscopy. Physical Review B. 2006;73(12). doi:10.1103/physrevb.73.125415
[141] Matsui T, Kambara H, Niimi Y, Tagami K, Tsukada M, Fukuyama H. STS Observations of Landau Levels at Graphite Surfaces. Physical Review Letters. 2005;94(22). doi:10.1103/physrevlett.94.226403
[142] Sugawara K, Sato T, Souma S, Takahashi T, Suematsu H. Fermi surface and edge-localized states in graphite studied by high-resolution angle-resolved photoemission spectroscopy. Physical Review B. 2006;73(4). doi:10.1103/physrevb.73.045124
Open Access
This article is licensed under a Creative Commons Attribution 4.0 International License. (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
© The Author(s) 2018

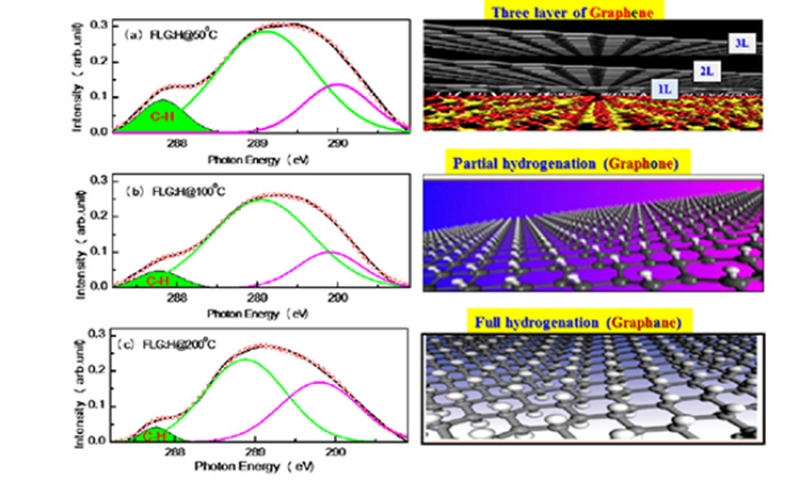
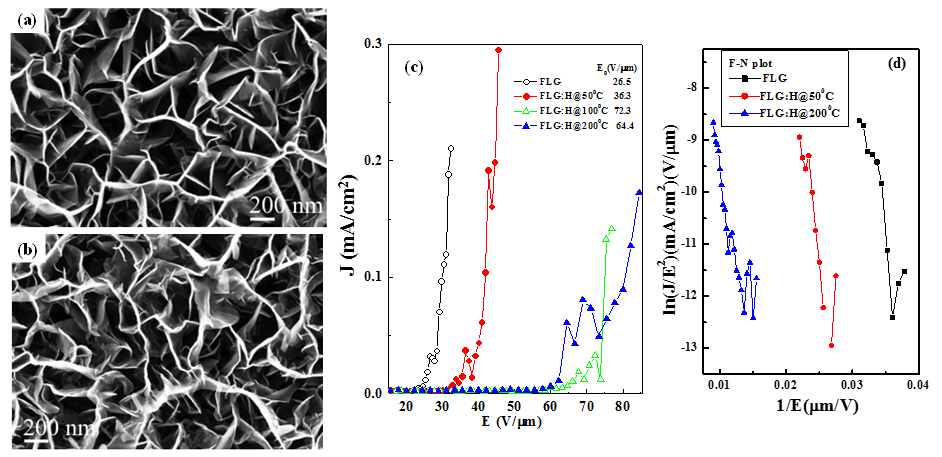
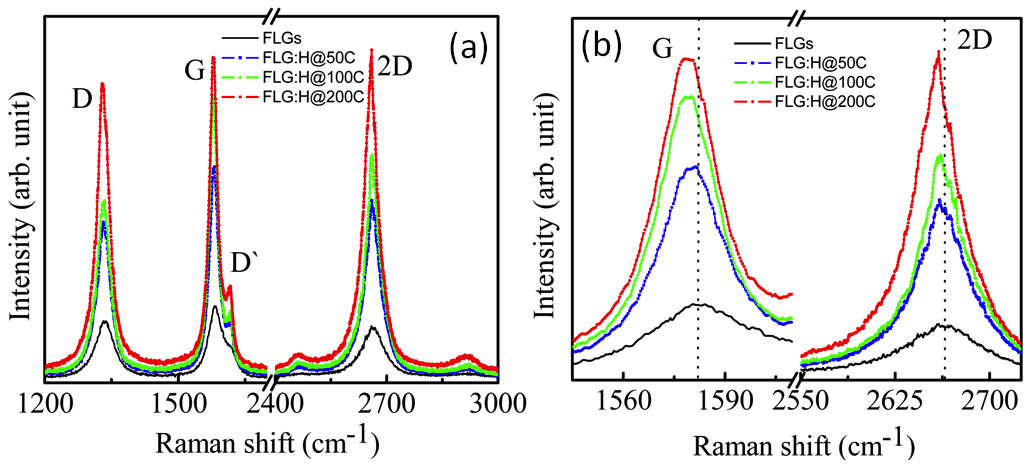
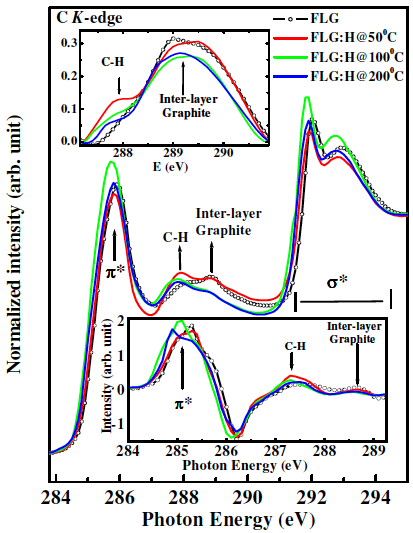
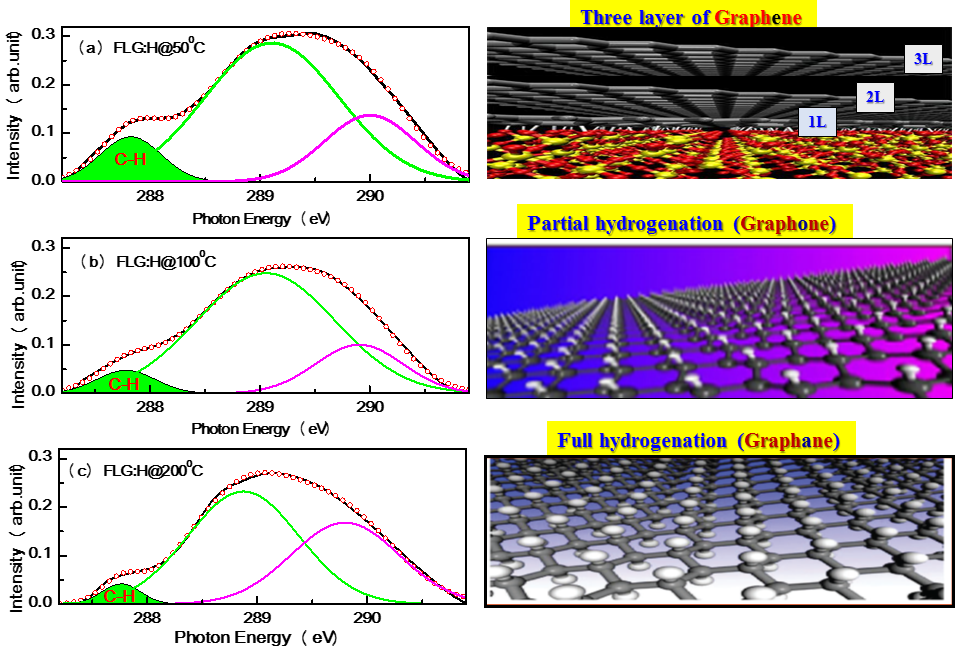
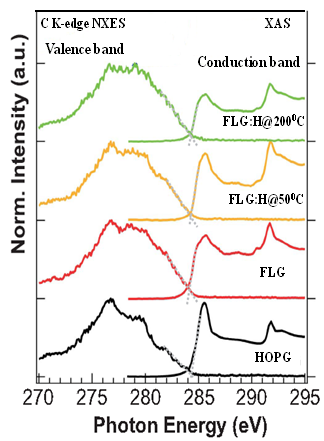
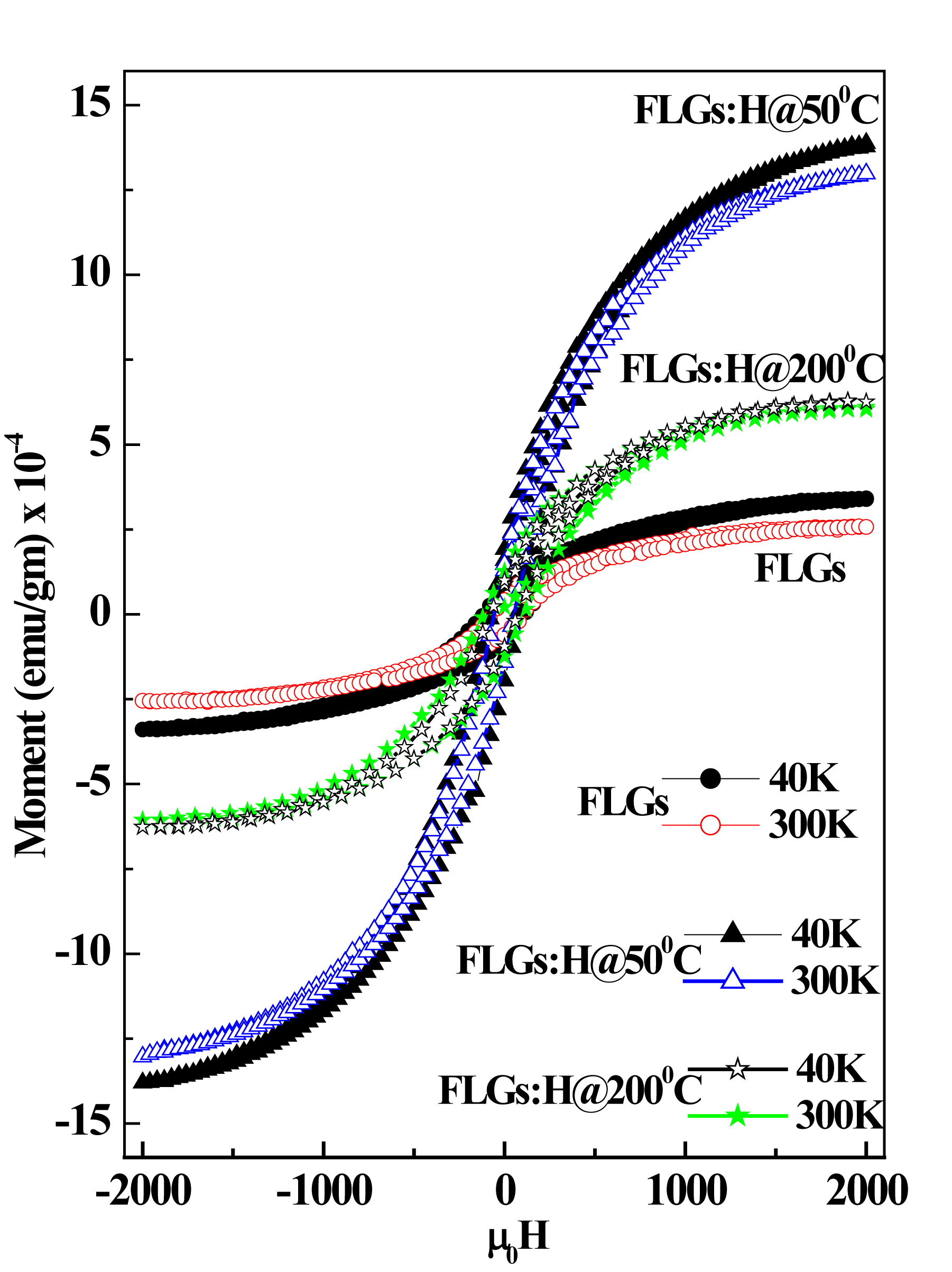
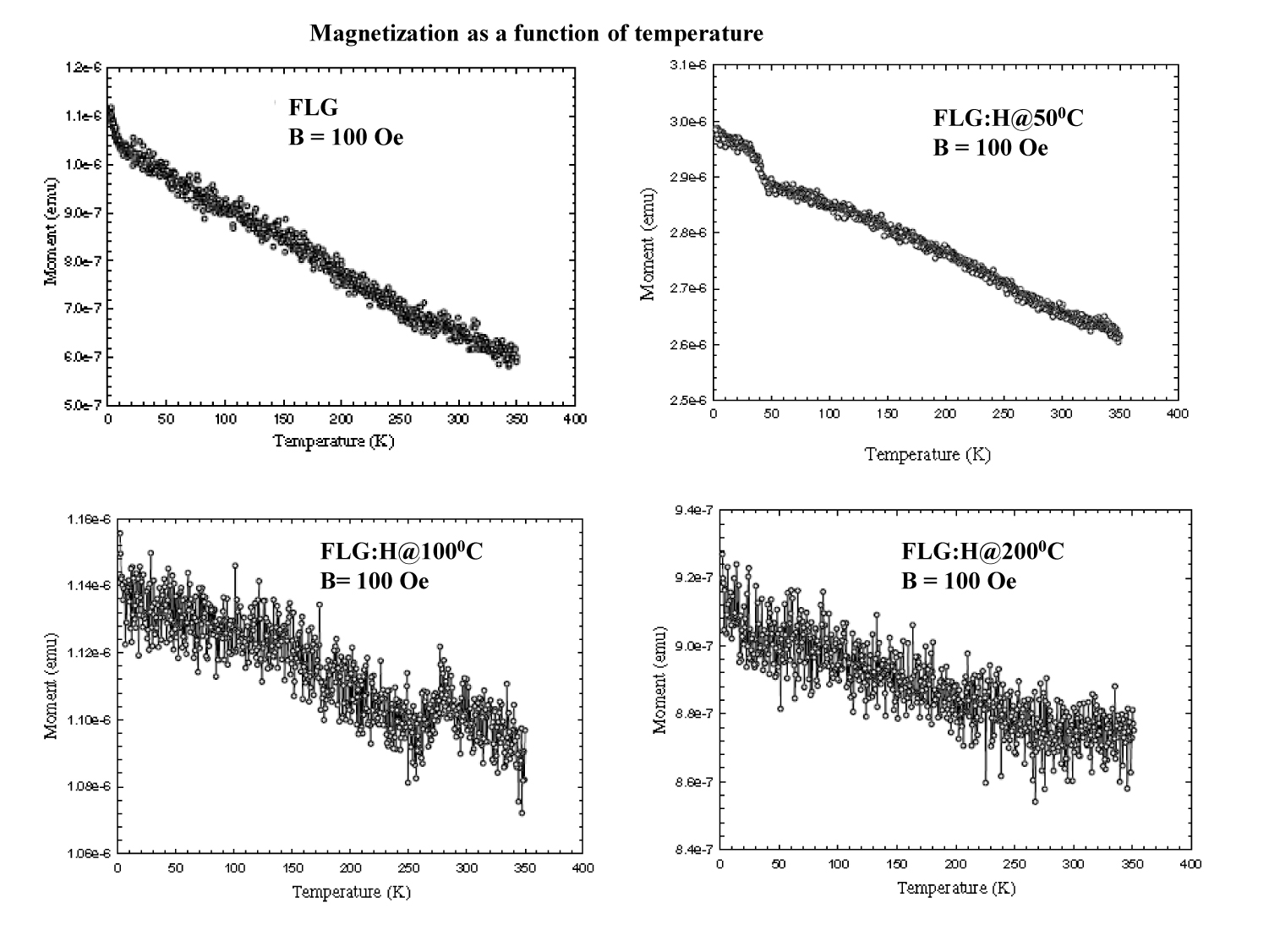
![Figure 8. Atomic Force Microscopy images of pristine (a-c) and hydrogenated FLGs [(d-f) @ 50oC and (g-i) @200oC].](/files/journal/frt/2018/01002/images/figure8_opt.jpg)
![Figure 9. Magnetic Force Microscopy images of pristine (a-c) and hydrogenated FLGs
[(d-f) @ 50oC and (g-i) @200oC].](/files/journal/frt/2018/01002/images/figure9_opt.jpg)
![(a) ideal graphene, (b) graphene with one atom vacancy, (c) graphene with one substitutional atom and (d) graphene with one ad-atom defect [Re-use with permission from Ref 97].](/files/journal/frt/2018/01002/images/figure11_opt.jpg)